200以上 場合の数 順列 組み合わせ 問題 107887-場合の数 順列 組み合わせ 問題

順列と組合せの違いと例題 高校数学の美しい物語
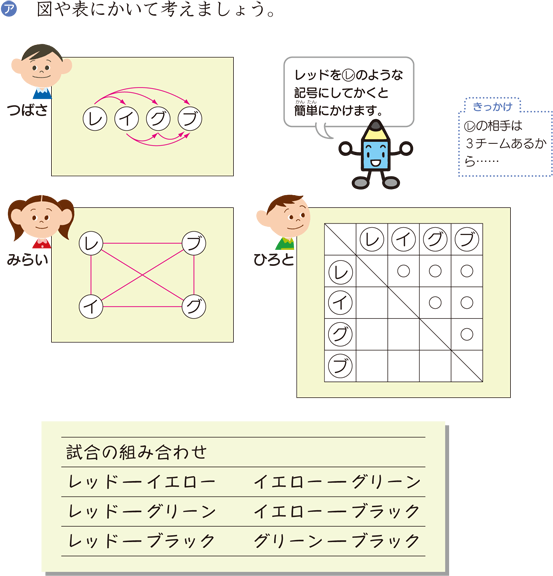
ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。 場合の数の勉強方法! 組み合わせと順列の解き方と勉強のコツ! 算数、数学と言っても、たいていの分野は公式を暗記することによってある程度を習得することができます。 「公式を暗記すること」と、「公式を問題に当てはめること」が比較
場合の数 順列 組み合わせ 問題
場合の数 順列 組み合わせ 問題-順列の公式は条件付き問題になったとたん、使い方が分からなくなる人が多いです。 公式丸暗記では今後対応しきれません。 上記の仕組みをきっちり理解してください! 全場合の数がどんな樹形図になるのか明確なイメージがわけば、どんなかけ算を 条件のある順列には、残念ながら 必殺技や公式 というものは存在しません。 強いていうなら、 「 条件の強いものから優先して並べろ 」です! し かし、入試問題には決まりきったパターンがあります。 条件付き順列のパターンを押さえて、その解き方やコツを覚えましょう!

順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
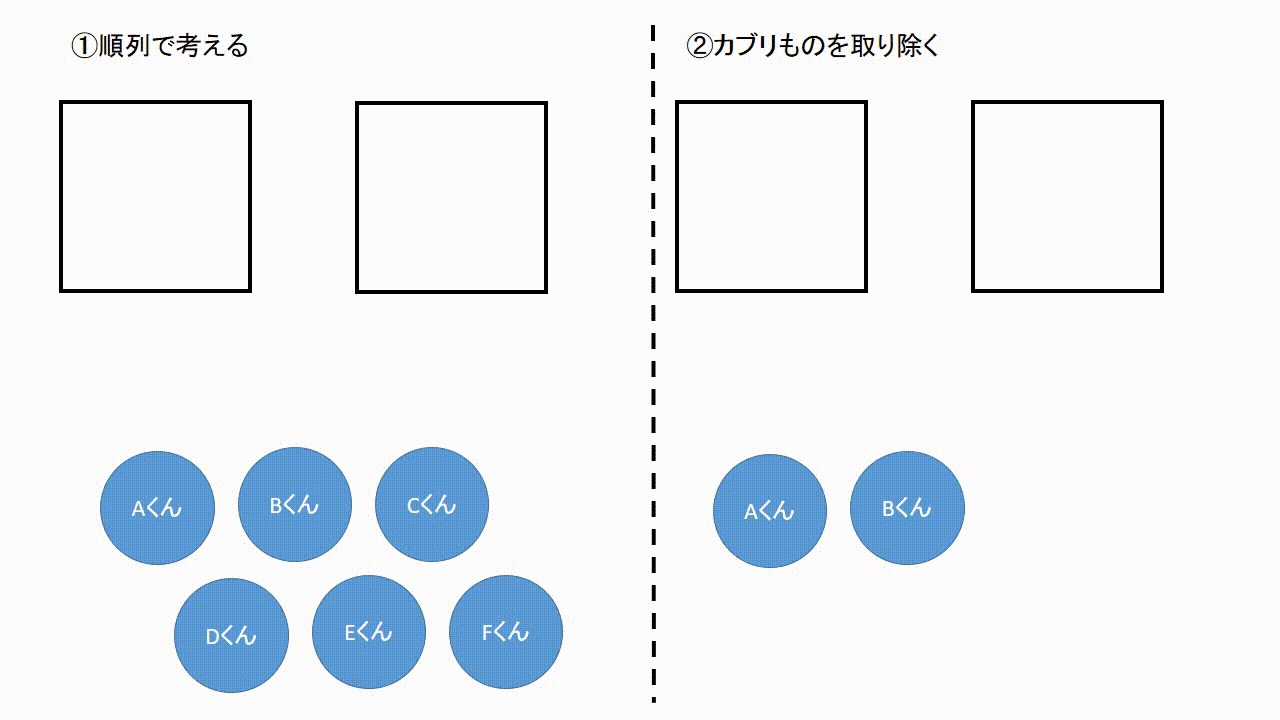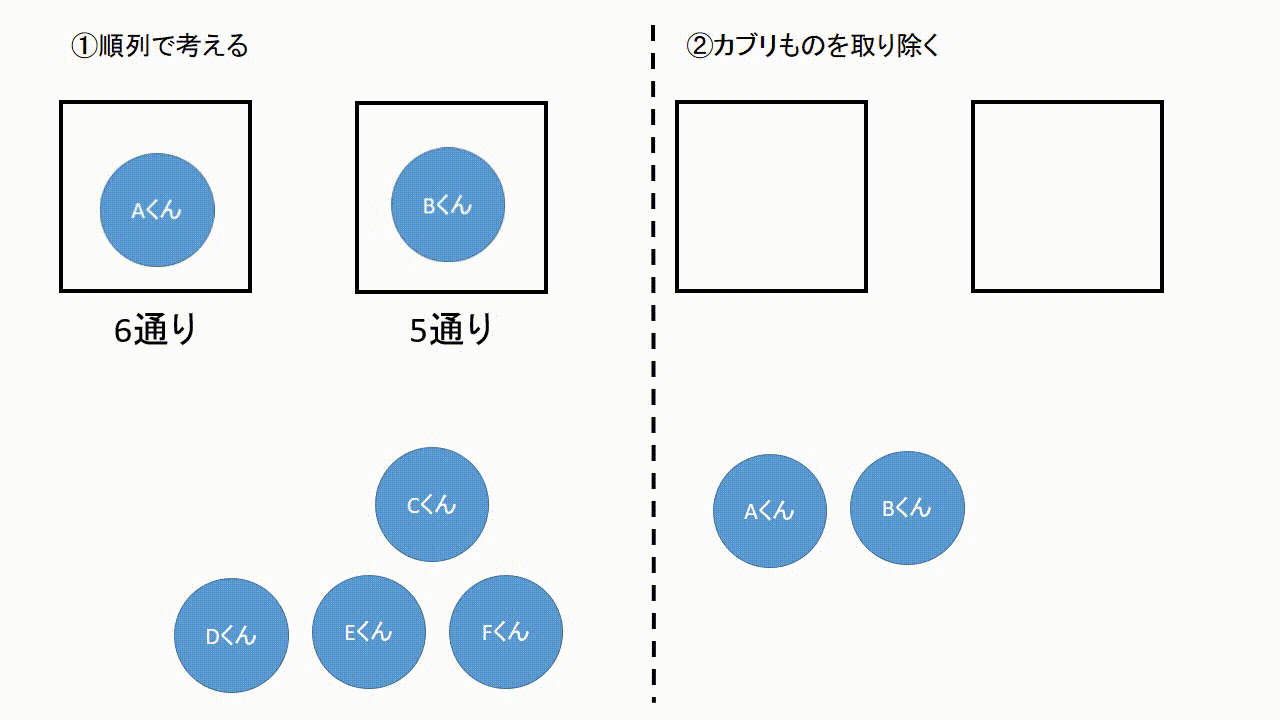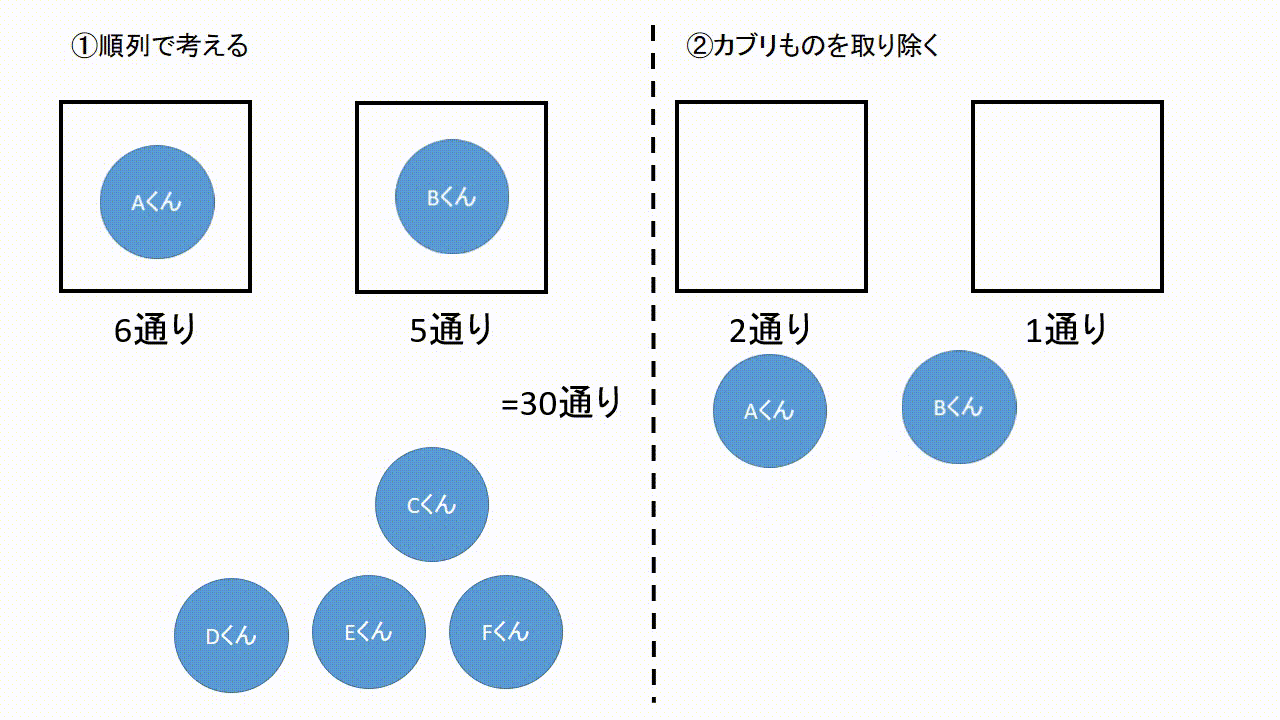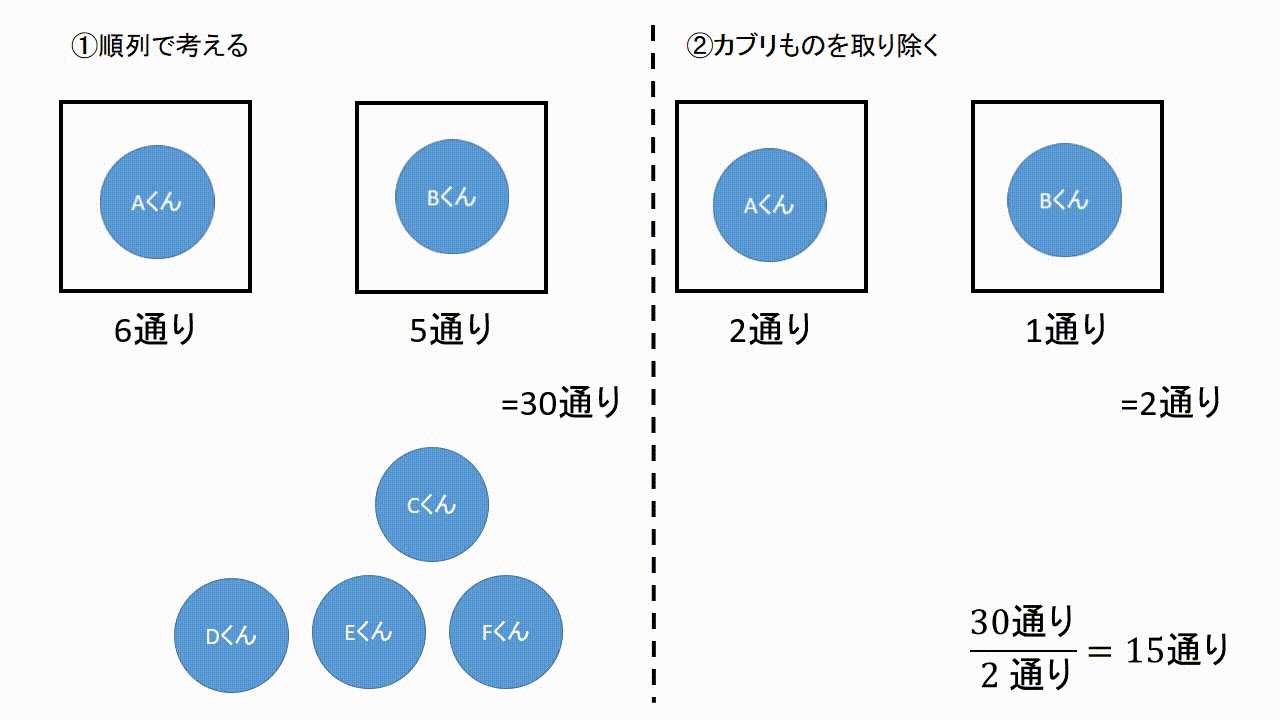
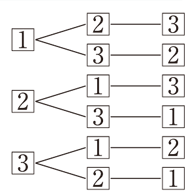
となる。 実際に、m=3 の場合に公式を適用すると、 n・ n-4 C 2 /3 となって当初の示唆に一致 することが確かめられた。 (問題補充3) 当HPがいつもお世話になっているHN「GAI」さんが、当HPの掲示板「出会 いの泉」に『微妙な違い』と題して次のような問題を出題された。場合の数の問題は大まかに分けると 順列 と 組み合わせ があり,これらは掛け算と割り算を駆使することで求めることができます. では実際に解いてみましょう!順列の問題(ならべ方)1 (1)男子2人に女子3人でリレーの順番を決めます。 ①全部で何通りの順番がありますか。 ②男子と女子が交互になる順番は何通りありますか。 (2)0 1 2 3の4枚のカードから3枚を並べて3けたの整数を作ります。 ①全部で何通りの整数ができますか。
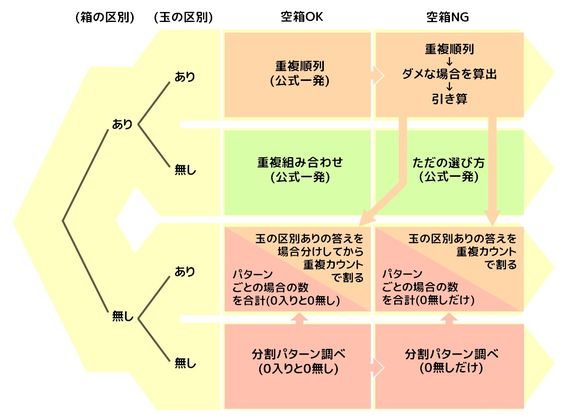
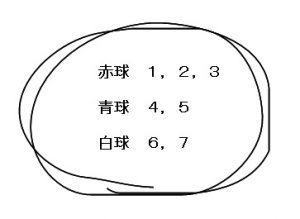
組合せとは いくつかのものからいくつかのものを取り出して並べることを順列と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は組合せの問題と呼ばれています. 順列 $\rightarrow$ 順序を考慮 (区別)する.N C r の関係があるが重複順列と重複組合せなどの関係は簡単ではない. 例 各位の数が異なる2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 P 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるかならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ・・・」 つまり、順序が問題になるので、『順列』の考えで。 4は「男子6人、女子10人の中から男子3人、女子4人
場合の数 順列 組み合わせ 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「場合の数 順列 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
しかし、この問題も、数ある頂点の中から4つの頂点を選ぶ問題だと思えば、場合の数の学習が応用できる。 横には4つの頂点が並んでいる。 4つの頂点から2つの頂点を選ぶと、横の辺が決まる。 同じように、 縦には5つの頂点が並んでいる。 高校数学 問題検索 数学A 場合の数と確率 「確率の基礎」 1,754 views 高校数学 解説動画 数学A 順列 辞書式配列 1,599 views スロット雑記 ~凱旋、ハーデスを打っていて思うこ
Incoming Term: 場合の数 順列 組み合わせ 問題,
コメント
コメントを投稿